საკითხები: გამრავლება; კანონზომიერება
მასალები: რვეული და კალამი
(7+7+7) x 37 = 777 მუშაობს, თუ არა ეს ხრიკი სხვა ერთნიშნა რიცხვებზე?
რატომ არის კარგი აქტივობა
ეს ამოცანები მოსწავლეებს საშუალებას აძლევს, ივარჯიშონ გამრავლებაზე და სიღრმისეულად გაიაზრონ მისი არსი. აღნიშნული აქტივობა ძალიან კარგი მოტივატორია მოსწავლეებისთვის, დაუკვირდნენ დეტალებს და უფრო კარგად დაეუფლონ თემას.
დაწყება
შენიშვნა: აქტივობა ჩაატარე მხოლოდ მაშინ, როცა დარწმუნდები, რომ ყველა შენმა მოსწავლემ იცის ორნიშნა რიცხვების გამრავლება.
სთხოვე მოსწავლეებს აირჩიონ ერთნიშნა რიცხვი, შემდეგ მიჰყევით ნაბიჯებს.
- მიუმატე ეს რიცხვი საკუთარ თავს 3-ჯერ.
- გაამრავლე შედეგი 37-ზე.
(პასუხი: ციფრი თავის თავს 3-ჯერ იმეორებს).
მაგალითად, თუ ჩავიფიქრეთ 7. ვუმატებთ: 7 + 7 + 7 და ვიღებთ 21-ს, შემდეგ ვამრავლებთ: 21 x 37. როდესაც ამას გამოვთვლით, მივიღებთ 777-ს. შეგვიძლია დავწეროთ (7 + 7 + 7) x 37 = 777. ეს არის 37-ის ძალა.
როდესაც აჩვენებ ერთ მაგალითს, ჰკითხე, ყოველთვის იმუშავებს, თუ არა ეს მიდგომა.
იქნება თუ არა (3 + 3 + 3) x 37 = 333? ან (9 + 9 + 9) x 37 = 999? შეუძლიათ მოსწავლეებს იპოვონ კონტრმაგალითი? თუ არა, რატომ მუშაობს ეს ხრიკი?
სამუშაო
მიეცი მოსწავლეებს საშუალება იმუშაონ დამოუკიდებლად, ან წყვილებში. შეამოწმებინე ეს ხრიკი ყველა ციფრისთვის. ამისთვის მათ დაახლოებით 15-25 წუთი უნდა დასჭირდეთ.
იმ მოსწავლეებისთვის, რომლებიც ადრე მორჩებიან, არსებობს ჩელენჯი, რომ შეამოწმონ ეს ხრიკი ორნიშნა რიცხვებისთვის: (10 + 10 + 10) x 37 იმუშავებს? ან (12 + 12 + 12) x 37?
სააზროვნო კითხვები
- რომელი რიცხვები სცადე?
- რა მიიღე?
- მანახე, როგორ გამოთვალე?
- შენი აზრით, შემდეგ რიცხვზეც იმუშავებს? რატომ/რატომ არა?
- რომელი რიცხვი დაარღვევს კანონზომიერებას?
შეჯამება
იმსჯელე მოსწავლეების აღმოჩენებზე. თუ ყველაფერი სწორად გამოთვალეს, ნახავდნენ, რომ ყველა ერთნიშნა რიცხვზე მუშაობს. მაგრამ რატომ?
რამდენიმე კარგი ახსნა არსებობს და მოსწავლეებს შეიძლება კიდევ ჰქონდეთ რაიმე აზრი:
ახსნა 1: (1 + 1 + 1) x 37 = 3 x 37 = 111 თუ შევცვლით ერთებს ორებით, შედეგიც გაორმაგდება და მივიღებთ 222-ს. იგივეა სამზე, ოთხზე და ასე შემდეგ ცხრის ჩათვლით.
ახსნა 2: (7 + 7 + 7) x 37 = (7 x 3) x 37 = 7 x ( 3 x 37) = 7 x (111) = 777 და იგივენაირად სხვა რიცხვებზეც.
ახსნა 3: ეს არის ვიზუალური ახსნა. ფართობის მეთოდის გამოყენებით 7 x 3 დავშალეთ შვიდ ცალ სამად (რაც იგივეა რაც 3 ცალი 7), შემდეგ კი ვაკვირდებით გამრავლებას.
რჩევები
- როდესაც მოსწავლეებს ეცოდინებათ, რომ ისინი ცდილობენ დებულების დადასტურებას ან უარყოფას და რაღაც არ ჯდება კანონზომიერებაში , სთხოვე გადაამოწმებინო საკუთარი პასუხი. თუ კანონზომიერება დაირღვევა, ძალიან მნიშვნელოვანია რომ პასუხი ზუსტი იყოს, ამიტომ გადამოწმება აუცილებელია.
- არ აჩვენო, რომ იცი, რომ ხრიკი ყოველთვის იმუშავებს, რათა მეტი მოტივაცია ჰქონდეთ.
- შეგიძლია ამ ამოცანას დაამატო გაყოფის ვერსიაც: თუ რომელიმე ციფრს გამოიყენებ 3-ჯერ სამნიშნა რიცხვის მისაღებად, შემდეგ გავყოფთ 3-ზე (სულ გაიყოფა ), შემდეგ კი ამავე ციფრზე, პასუხად მივიღებთ… 37? მაგალითად, 777 ÷ 3 = 259. შემდეგ 259 ÷ 7, რაც არის 37!, ან: 444 ÷ 3 = 148. და 148 ÷ 4 = 37 ისევ! თუ მოსწავლეებს ესმით კავშირი გამრავლებასა და გაყოფას შორის, მალევე აუღებენ ალღოს, თუმცა ბევრმა მოსწავლემ შეიძლება ინტუიტიურად ვერ დააკავშიროს ეს ორი და დასჭირდეს შემოწმება, რათა დარწმუნდეს, რომ პასუხი 37-ია.
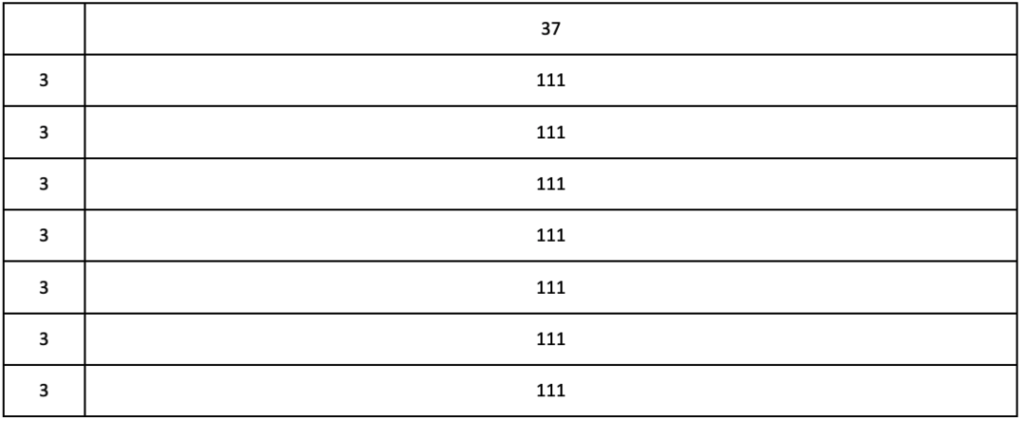
- თუ გინდა, შეგიძლია გამოიყენო ქვემოთ მოცემული სამუშაო ფურცელი, სადაც მაგალითია: (7 + 7 + 7) × 37 = 777.