საკითხები: ალგებრა; მიმატება; გამოკლება; გამრავლება; გაყოფა; წილადები; ათწილადები; უარყოფითი რიცხვები; ამოცანა; კონტრარგუმენტები; დაშვებები
მასალები: ფურცლები; კალმები; დაფა; ერთეულების ჯოხები (არჩევითად); სამუშაო ფურცლები (არჩევითად – ნახე ქვემოთ); ვიდეოები (არჩევითად):
ნაწილი 1: https://www.youtube.com/watch?v=n2RTjqHUXGQ
ნაწილი 2: https://www.youtube.com/watch?v=HMSmt5yOl6E
როგორ ხდება ისე, რომ სულ ერთი და იგივე გამოდის?
რატომ არის კარგი აქტივობა
ამ მარტივ ხრიკს შეუძლია ფართოდ დიფერენცირება. გამოდგება უარყოფითი რიცხვების გამოკლებაზე, წილადების გაყოფაზე, არითმეტიკაზე, ან მთელ რიცხვებზე სავარჯიშოდ.
დაწყება
აუხსენი ფოკუსი მოსწავლეებს. თითოეული მოსწავლე უნდა მიჰყვეს ინსტრუქციას:
- ჩაიფიქრე მთელი რიცხვი 1-დან 10-მდე.
- მიუმატე 2.
- გაამრავლე 2-ზე.
- გამოაკელი 2.
- გაყავი 2-ზე.
- გამოაკელი ის რიცხვი, რაც ჩაიფიქრე.
ყველას საბოლოო პასუხი უნდა იყოს 1 (იმის დაშვებით, რომ თვლისას შეცდომა არ დაუშვიათ).
დიდი შეკითხვა: იმუშავებს, თუ არა ეს ისეთ რიცხვებზე, რომლებიც არ არიან მთელები და არ არიან 1-სა და 10-ს შორის? რა რიცხვებზე იმუშავებს?
სამუშაო
მოსწავლეების უმრავლესობისთვის ამ პატერნის „გატეხვა“ დიდი გამოწვევაა. შეუძლიათ სცადონ დიდი რიცხვები, უარყოფითი რიცხვები, წილადები, ათწილადები, ან ნებისმიერი სხვა რიცხვი, რაც იციან.
შეაგროვე დაშვებები, თუ რა რიცხვი შეიძლება ჩაიფიქროს ადამიანმა, რომ 1 არ ამოვიდეს ფოკუსის შედეგად. გამოიყენე დრო რომ ჩართო მოსწავლეები.
სააზროვნო კითხვები
- შენი აზრით, რა რიცხვი გატეხავს პატერნს?
- შენი აზრით, 17 იმუშავებს? მოდი ერთად ვცადოთ.
- რომელი რიცხვი არ იმუშავებს? მოდი რამდენიმე ჩამოვწეროთ და მერე ვცადოთ.
- დიდი რიცხვები სცადე? მაგალითად 40156?
- უარყოფითი რიცხვები იმუშავებს? მაგალითად -5?
- შენი აზრით, წილადებზეც იმუშავებს? მაგალითად 12?
- ათწილადებზეც იმუშავებს? მაგალითად 6.7?
- ყველაზე უცნაური რა რიცხვი გახსენდება? მაგალითად π?
- რატომ ფიქრობ რომ ყოველთვის იმუშავებს? ვინაიდან რაც ვცადეთ ჯერ-ჯერობით ყველაფერზე მუშაობს?
- მაინტერესებს, შეგვიძლია ალგებრა დავიხმაროთ?
- (მოსწავლეებისთვის, ვინც სრულად ამოხსნა ამოცანა) რა მოხდება, თუ ყველა 2-ს 3-ით ჩავანაცვლებთ? მაინც იმუშავებს?
შეჯამება
როდესაც მოსწავლეები რამდენიმე მაგალითს განიხილავენ, დასვი შემდეგი შეკითხვა:
რატომ მუშაობს ეს ყოველთვის?
ამ მომენტისთვის, ეს შეკითხვა შეუძლებლად რთული ჩანს. იმის საჩვენებლად, რომ ყოველთვის მუშაობს, მაგიური ფოკუსი ყველა რიცხვისთვის უნდა დატესტო, რაც ნიშნავს რომ უსასრულოდ ბევრი სამუშაოა. ასეთ დროს როგორ დავამტკიცოთ, რომ რაიმე ყოველთვის მუშაობს / ან არ მუშაობს?
დარჩენილი დროის მიხედვით, აარჩიე, ამ შეკითხვაზე დიდ დროს მისცემ, თუ შემდეგ გაკვეთილზე დაუბრუნდები ამ საკითხს. ამის ამოსახსნელად შეგიძლია გამოიყენო უჯრების მოდელი, ან ერთეულების ჯოხები. აირჩიე ნებისმიერი ჯოხი, ან დახატე ცარიელი უჯრა. დაუშვით, რომ ეს არის რაიმე რიცხვი, ოღონდ ჯერ არავინ არ ვიცით თუ რა რიცხვია ეს.
გააკეთე მაგიური ფოკუსი უჯრაზე და გამოიყენე სათვლელები ერთეულებისთვის.
მიუმატე 2:
გაამრავლე 2-ზე:

გამოაკელი 2:
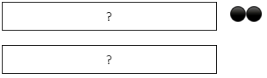
გაყავი 2-ზე:
გამოაკელი ის რიცხვი, რაც ჩაიფიქრე:
აი ეს არის ალგებრული ფიქრის ძალის დემონსტრაცია! მნიშვნელობა არ აქვს რა იყო უცნობი რიცხვი, რა ეწერა სინამდვილეში უჯრაში, საბოლოო შედეგი ყოველთვის იქნება 1.
როდესაც უჯრაში ვტოვებთ კითხვის ნიშანს, რეალურად ვამოწმებთ ყველა რიცხვს ერთდროულად!
იგივე სამუშაო შეგვიძლია ჩავატაროთ ალგებრის გამოყენებით. იმ მოსწავლეებისთვის, ვინც ჯერ თავს კომფორტულად არ გრძნობს ალგებრასთან, ეს მაგიური ფოკუსი კიდევ ერთ შანსს სთავაზობს პრინციპის გასაგებად.
მაგალითად, ხშირად ამისთვის იყენებენ პი-ს. ვინაიდან, ბევრმა მოსწავლემ იცის, რომ პი-ს ციფრები გრძელდება უსასრულოდ გამეორების გარეშე, ჩვენ არ შეგვიძლია მისი სრულად ჩაწერა. სამაგიეროდ, ჩვენ შეგვიძლია ჩავწეროთ მხოლოდ ასო! რაც მოგვცემს ამას:
- π (აირჩიე რიცხვი)
- π + 2 (დაუმატე 2)
- 2 π + 4 (გაამრავლე 2-ზე… ეს ნაბიჯი შეიძლება ცოტა რთული იყოს მათთვის, ვინც არ იცის ალგებრა)
- 2 π + 2 (გამოაკელი 2)
- π + 1 (გაყავი 2-ზე)
- 1 (გამოაკელი ჩაფიქრებული რიცხვი)
შენიშვნა: ამ გადასვლაზე შეგიძლია ნახო ვიდეო ინსპირაციისთვის
თუმცა აქ არის ალგებრის დიდი იდეა: ჩვენ არ გვჭირდება, რომ რამე ვიცოდეთ π-ს შესახებ იმისთვის, რომ გავიგოთ, რომ პასუხია 1. რეალურად, π შეიძლება ყოფილიყო ნებისმიერი რიცხვი და ჩვენ მაინც იგივეს მივიღებდით. მოიცა… თუ π შეიძლება ყოფილიყო ნებისმიერი რიცხვი და ფოკუსი მაინც იმუშავებდა, ესეიგი ეს ფოკუსი ყველა რიცხვზე მუშაობს! ეს რეალურად არის ალგებრული დამტკიცება, რომელიც გვაძლევს არგუმენტს, რომ ფოკუსი ყოველთვის მუშაობს. კარგი იქნება თუ მოსწავეებს ეტყვი, რომ ადამიანები ყველაზე ხშირად მსგავსი საკითხებისთვის იყენებებნ x-ს და არა π-ს.
- x (აირჩიე რიცხვი)
- x + 2 (მიუმატე 2)
- 2 x + 4 (გაამრავლე 2-ზე… ეს ნაბიჯი შეიძლება ცოტა რთული იყოს მათთვის, ვინც არ იცის ალგებრა)
- 2 x + 2 (გამოაკელი 2)
- x + 1 (გაყავი 2-ზე)
- 1 (გამოაკელი ჩაფიქრებული რიცხვი)
ამის შემდეგ, ფოკუსის განზოგადებას მივყავართ ბუნებრივ განვრცობებამდე, რომელიც მომავალ შეხვედრებზე გამოგვადგება. შეგიძლია მოსწავლეებს მისცე დავალებად, ან სხვა გაკვეთილზე განიხილოთ შემდეგი კთხვები.
შეკითხვა: რა მოხდება თუ ფოკუსს ცოტათი შევცვლით?
ვარიაცია
- ჩაიფიქრე ნებისმიერი რიცხვი.
- მიუმატე 4.
- გაამრავლე 4-ზე.
- გამოაკელი 4.
- გაყავი 4-ზე.
- გამოაკელი ის რიცხვი რაც ჩაიფიქრე.
ყოველთვის ერთი და იგივე პასუხს მიიღებ?
რა თქმა უნდა, მოსწავლეებს შეილება ჰქონდეთ თავისი იდეები, როგორ შეცვალონ ფოკუსი. კარგია, თუ ექსპერიმენტების საფუძველზე თვითონ შეამოწმებენ საკუთარ იდეებს. რა ცვლილებების შემთხვევაში იცვლება ფოკუსის შედეგი და რა შემთხვევაში არა. კარგია თუ ამ ყველაფერს ალგებრით ან ჩანახატით შეამოწმებენ.
რჩევები
- ამ ფოკუსის მთავარი იდეაა, რომ მოსწავლეებმა მაშინვე ვერ გაიგონ პასუხი. შესთავაზე მაქსიმალურად ბევრი ვარიანტი (წილადები, უარყოფითი რიცხვები…), სანამ დაინტერესებულები იქნებიან. ხაზი გაუსვი, თუ რამდენად რთულია თითოეული ახალი ვარიაციის შემოწმება. არ დააჩქარო ის მოსწავლეები, რომლებზეც გრძნობ, რომ ჯერ მზად არ არიან.
- ზოგმა მოსწავლემ შეიძლება დაუშვას არითმეტიკული შეცდომა და ეგონოთ, რომ მათ იპოვეს კონტრმაგალითი. მიეცი საშუალება, რომ ერთმანეთის დაშვებები შეამოწმონ.
- არ არის აუცილებელი, რომ მაინც და მაინც ახსენო „x“, ან დაამტკიცო, რომ ფოკუსი ყოველთვის მუშაობს. ზოგი კლასისთვის შეიძლება უკეთესიც იყოს, თუ ფოკუსი ჯადოქრობად დარჩება. ეს აწევს მოტივაციას არითმეტიკაში!
- ქვემოთ მოცემული ფურცლები არის ვიზუალური მასალა დაწყებისთვის, თუმცა ისინი აბსოლუტურად არჩევითია. უკეთესი იქნება თუ ამ ყველაფერს დაფაზე მოსწავლეებთან ერთად გააკეთებ და არა, უბრალოდ აჩვენებ.