საკითხები: ტოლობა; ჩანაცვლება; მიმატება; გამოკლება
მასალები: პატერნის ბლოკები; ფანქარი და ფურცელი; დააბალანსე სასწორი – სამუშაო ფურცელი (არასავალდებულო)
რამდენი ბლოკია საჭირო გასათანაბრებლად?
რატომ არის კარგი აქტივობა
ეს გაკვეთილი კონკრეტული არითმეტიკული პრაქტიკის დახმარებით, ხელს უწყობს მოსწავლეებს, კონცეპტუალურად აღიქვან ტოლობა და ერთეულების ჩანაცვლება.
დაწყება
დასაწყისში საჭირო იქნება მოსწავლეებს დაეხმარო მიხვდნენ, თუ როგორ უნდა გაათანაბრონ ორი მხარე სხვადასხვა ბლოკების გამოყენებით.
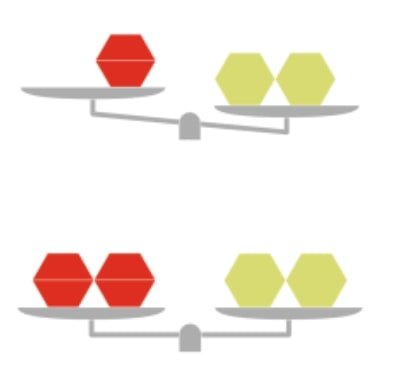
მასწავლებელი: მე თუ ორ ექვსკუთხედს დავდებ ამ მხარეს, საჭირო იქნება მეორე მხარეს დავდო 2 ტრაპეცია, რადგან 2 ბლოკი 2 ბლოკის ტოლია. (მოსწავლეები შესაძლოა თავიდანვე არ დაგეთანხმონ). აბა შევამოწმოთ. (დადეთ ტრაპეციები ისე, რომ გამოვიდეს ექვსკუთხედი). როგორც ჩანს, არ გათანაბრდა, იმიტომ რომ უფრო ნაკლებ ადგილს იკავებს. რამდენი ტრაპეცია დამჭირდება, რომ 2 ექვსკუთხედის ტოლი გახდეს?
მოსწავლე: 4 ტრაპეცია
მასწ.: რატომ 4?
მოსწ.: იმიტომ, რომ 1 ექვსკუთხედი 2 ტრაპეციაა და 2+2=4.
მასწ.: გაგასებია. მოდი, ვცადოთ ასე თუ გამოვა. (ვალაგებთ, როგორც მოსწავლემ გვიკარნახა). ძალიან კარგი.
აბა რამდენი რომბი დაგვჭირდება, რომ 2 ექვსკუთხედის ტოლი იყოს? ცოტახანს დაფიქრდით, შემდეგ კი, როცა პასუხს მოიფიქრებთ, განიხილეთ თქვენს გვერდით მჯდომ კლასელთან.
მოსწ.: (ფიქრის შემდგომ) – 6.
მასწ.: 6 რა?
მოსწ.: 6 რომბი.
მასწ.: შენ ფიქრობ, რომ 6 რომბი იგივეა, რაც 2 ექვსკუთხედი?
მოსწ.: კი.
მასწ.: რატომ?
მოსწ.: იმიტომ, რომ 1 ექვსკუთხედი იგივე 3 რომბია.
მასწ.: აბა მაჩვენე. (მოსწავლე ექვსკუთხედზე დებს 3 რომბს). აჰა, როგორც ვნახეთ, 1 ექვსკუთხედი არის 3 რომბის ტოლი, მეორე ექვსკუთხედიც ასევე, ანუ ორი ექვსკუთხედი იქნება 3+3 რომბი. მოდი, აბა, ვნახოთ. (ვდებთ 6 რომბს და 2 ექვსკუთხედს). კი, თანაბარია.
მასწ.: კარგი, ახლა ბოლო. რამდენი სამკუთხედი იქნება საჭირო 2 ექვსკუთხედის შესავსებად? ცოტახანს დაფიქრდით.
მოსწ.: 12 სამკუთხედი!
მასწ.: მოდი, შევამოწმოთ. (ვალაგებთ სამკუთხედებს ისე, რომ გამოვიდეს 2 ექვსკუთხედი). კი ბატონო. ახლა დროა, თქვენით სცადოთ.
მე შემოგთავაზებთ რამდენიმე განსხვავებულ ვარიანტს და თქვენ გადაწყვიტეთ რომელს აირჩევთ. და თუ ნამდვილი გამოწვევა გინდათ, იფიქრეთ, რამდენი სამკუთხედი იქნება საჭირო.
შეგიძლიათ იმუშავოთ 2, ან 3კაციან ჯგუფებში. პასუხი მითხარით მაშინ, როდესაც ჯგუფის ყველა წევრი დარწმუნებული იქნება და შემდგომ ერთად შევამოწმოთ. მზად ხართ?
ესეც პირველი გამოწვევა: მაქვს 5 ექვსკუთხედი, თქვენ კი ახლა უნდა გაარკვიოთ ერთ-ერთი:
- რამდენი ტრაპეცია იქნება საჭირო ორი მხარის გასათანაბრებლად, ან
- რამდენი რომბი იქნება საჭირო, ან
- რამდენი სამკუთხედი იქნება საჭირო
თუ სურვილი გაქვთ, შეგიძლიათ სამივეზე მიპასუხოთ.
სამუშაო
ნელ-ნელა გაზარდეთ ბლოკების რაოდენობა. თითოეულ შემთხვევაში, მოსწავლეებმა უნდა გაიგონ, რამდენი ტრაპეცია (უფრო მარტივია), რამდენი რომბი (საშუალო), ან რამდენი სამკუთხედია (უფრო რთული) საჭირო გასათანაბრებლად. თავისუფლად შეგიძლიათ მოსწავლეებს რამდენიმე ვარიანტი ერთდროულად მისცეთ, რომ დამოუკიდებლად ამოხსნან პრობლემათა სერიები. ან შეგიძლიათ სხვადასხვა ჯგუფს განსხვავებული ვარიანტები დაურიგოთ, იმის შესაბამისად, თუ რა სირთულისთვის არიან მზად.
გამოწვევები: გაარკვიე რამდენი ტრაპეცია/რომბი/სამკუთხედია საჭირო, რომ დააბალანსო:
ა) 2 ექვსკუთხედი
ბ) 3 ექვსკუთხედი
გ) 5 ექვსკუთხედი
დ) 10 ექვსკუთხედი
ე) 15 ექვსკუთხედი
ვ) 4 ექვსკუთხედი + 4 ტრაპეცია
ზ) 3 ექვსკუთხედი + 3 ტრაპეცია + 3 რომბი
თ) 4 ექვსკუთხედი + 4 ტრაპეცია + 4 რომბი + 4 სამკუთხედი
სააზროვნო კითხვები
- რატომ გგონია, რომ ეს გაათანაბრებს?
- რა მოხდება, თუ ვცდით 8 ტრაპეციას 5 ექვსკუთხედის საპირწონედ? თქვენი აზრით, გაუტოლდება? თუ მეტი იქნება? თუ ნაკლები? მოდი ვცადოთ.
- თქვენით მოიფიქრეთ რაიმე გამოწვევა ჩემთვის, ან თქვენი კლასელებისთვის.
შეჯამება
აირჩიეთ ბოლო პრობლემა, რომელსაც ყველა მოსწავლე შეასრულებს და სთხოვეთ მათ, აგიხსნან, თუ როგორ ფიქრობენ/ვარაუდობენ.
მაგალითად, თუ უნდათ, რომ 10 ექვსკუთხედის საპირწონედ დადონ რამდენიმე რომბი, გაგიზიარონ, როგორ მიხვდებიან, რამდენი რომბი იქნება საჭირო.
რჩევები
- თუ გაქვთ სასწორი, შეგიძლიათ გამოიყენოთ კლასში. უბრალოდ დარწმუნდით, რომ ყველა პატერნის ბლოკი ერთი და იმავე კომპლექტიდან იქნება და მართლა მაშინ გათანაბრდება, როცა შესაბამისი რაოდენობის ბლოკებს დაალაგებთ.
- პრობლემათა მიმდევრობა შეგიძლიათ დაალაგოთ საჭიროების მიხედვით. ასევე კარგი იქნება, თუ მოსწავლეები თავად მოიფიქრებენ ამ ტიპის პრობლემებს და ამოხსნიან, ან გაუზიარებენ ერთმანეთს.
- თუ ბავშვების სისწრაფეს აყვები, შეძლებ შეამოწმო თითოეული ამოხსნა მანამ, სანამ ჯგუფს ახალ გამოწვევას მისცემ. თუმცა, მოსწავლეები არ უნდა ისხდნენ და ელოდონ, რომ შენ შეამოწმო მათი პასუხები, იმისათვის, რომ გადავიდნენ ახალ საკითხზე, თუ ვერ ასწრებ, მიეცი მათ პირდაპირ ახალი გამოწვევა