საკითხები: გაყოფა; ერთეულების ცვლა
მასალები: პატერნის ბლოკები; ფურცელი და ფანქარი
ეს არის პატერნის ბლოკებით გამრავლების შებრუნებული აქტივობა. იცი დიდი ფიგურა… როგორ შეგიძლია დათვალო ცალკეული ნაწილები?
რატომ არის კარგი აქტივობა
ეს გაკვეთილი ერთმანეთთან აკავშირების გაყოფისა და პრობლემების გადაჭრის ძირითად პრინციპებს. კარგი გზაა, რომ გააგრძელო თანაბარ განაწილებაში დაწყებულ საკითხებზე მუშაობა უფრო რთულ და დახვეწილ, თუმცა ისევ ხელშესახებ და შინაარსიან კონტექსტში.
დაწყება
მასწავლებელი აჯგუფებს პატერნის ბლოკებს, ამბობს მათ მნიშვნელობებს და სვამს შეკითხვებს, მოსწავლეები კი დამოუკიდებლად ცდილობენ ამოხსნას და პასუხების ჩაწერას.
მიეცი მოსწავლეებს იმდენი დრო, რამდენიც სჭირდებათ – მინიმუმ 1, ან 2 წუთი საწყის ეტაპზე და ცოტა მეტი უფრო რთულ შეკითხვებზე.
შეკითხვა 1: თუ სამი ექვსკუთხედი ერთად უფრის 18-ს, რას უდრის 1 ტრაპეცია?
შენიშვნა: შეგიძლია წარადგინო პრობლემები სიტყვებს გარეშეც, უბრალოდ დაალაგე პატერნის ბლოკები დაფაზე და მიუწერე მნიშვნელობები.
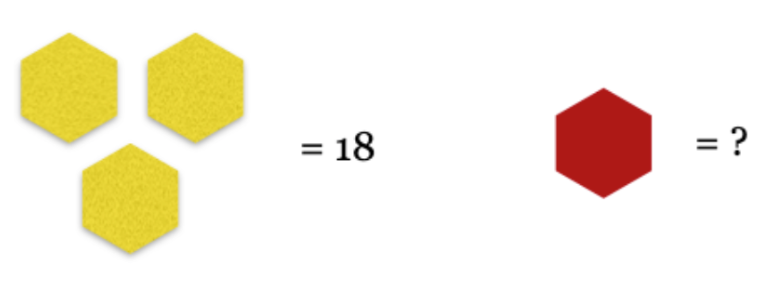
პასუხი: ტრაპეცია = 3
შესაძლო ახსნა: თუ 3 ექვსკუთხედი = 18, მაშინ 1 ექვსკუთხედი = 18:3=6
(რადგან 3 ცალი 6-ეულის ჯგუფი არის 18, 3 x 6 = 18). იქიდან გამომდინარე, რომ ტრაპეცია არის 6-ის ნახევარი, პასუხი უნდა იყოს 3.
მნიშვნელოვანია, რომ ამის შემოწმება შეგვიძლია გამრავლების საშუალებით.
თუ ტრაპეცია = 3, რამდენი გამოვა 3 ექვსკუთხედი?
შეკითხვა 2: თუ 2 ექვსკუთხედს + 1 ტრაპეცია = 20, რას უდრის 1 ტრაპეცია?

პასუხი: ტრაპეცია = 4
შესაძლო ახსნა: შეგვიძლია ექვსკუთხედები წარმოვადგინოთ ტრაპეციებად, მაშინ გვექნება 5 ტრაპეცია = 20, საიდანაც გავიგებთ, რომ თითოეული უნდა უდრიდეს 4-ს, რადგან 5 x 4 = 20.
შემდეგ ეტაპებზე მოსწავლეებს, რომლებიც მზად იქნებიან უფრო რთულ პრობლემებზე სამუშაოდ, შეუძლიათ ამოხსნან ბონუს პრობლემები და გაიგონ, რა იქნება რომბის, ან სამკუთხედის მნიშვნელობა. თუ ბევრ მოსწავლეს არ ექნება განცდა, რომ არ ესმით კარგად, შეგიძლია ყოველი შემთხვევა ცალ-ცალკე აღარც განიხილო.
შეკითხვა 3.
4 ექვსკუთხედი =36 1 ტრაპეცია = ? (ბონუსი: რომბი = ? სამკუთხედი = ?)
შეკითხვა 4.
5 ექვსკუთხედი =60 1 ტრაპეცია = ? (ბონუსი: რომბი = ? სამკუთხედი = ?)
შეკითხვა 5.
3 ექვსკუთხედს + 3 ტრაპეცია = 27 1 ტრაპეცია = ? (ბონუსი: რომბი = ? სამკუთხედი = ?)
შეკითხვა 6.
4 ექვსკუთხედს + 5 ტრაპეცია = 52 1 ტრაპეცია = ? (ბონუსი: რომბი = ? სამკუთხედი = ?)
თუ მეტი შეკითხვაა საჭირო, მოსწავლეებს შეუძლიათ თავად მოიფიქრონ და გამოიწვიონ ერთმანეთი.
სააზროვნო კითხვები
- რა იქნება ტრაპეცია რომ 5-ს უდრიდეს? ეს ძალიან ბევრია, თუ ძალიან ცოტა?
- თუ 4 ექვსკუთხედი = 36, რისი ტოლი იქნება 2 ექვსკუთხედი?
შეჯამება
აირჩიე ბოლო პრობლემა, რომელზეც ყველა მოსწავლემ იმუშავა და დაუთმე რამდენიმე წუთი ამის განხილვას. მიეცი საშუალება, რომ ერთმანეთს გაუზიარონ ამოხსნის გზები. შესაძლებელია, რომ მათი სტრატეგიები გაუზიარონ მეწყვილეებს, შემდეგ შეარჩიო 1, ან 2 მოხალისე და გაუზიარონ ეს მეთოდები კლასს.
რჩევები
- დარწმუნდი, რომ მოსწავლეებს შეუძლიათ შეადგინონ და ამოხსნან პრობლემის თავიანთი ვერსია.
- ცვალე პრობლემათა სირთულე, რამდენადაც საჭირო იქნება.
- მოსწავლეებს ყოველთვის შეუძლიათ, რომ გამოიცნონ პასუხი და შემდეგ შეამოწმონ. ეს კარგი სტრატეგიაა წასახალისებლად, რადგან უფრო ნათელს ხდის გაყოფასა და გამრავლებას შორის კავშირს.