საკითხები: გამრავლება; მიმატება; პრობლემების გადაჭრა
მასალები: კალენდარი; ფურცელი და ფანქარი; ასობითი ცხრილი
როგორ შეიძლება კალენდარზე რიცხვების ძალიან სწრაფად შეკრება?
რატომ არის კარგი აქტივობა

სათამაშოდ ძალიან მარტივია და გამოწვევებით სავსე. ეს აქტივობა მოიცავს კალენდრის გამოყენებას, რაც რეალურ ცხოვრებასთან კავშირშია და მოსწავლეებს უფრო მეტად აინტერესებთ. გარდა ამისა, ეს თავსატეხი გამრავლების უნარის სარგებლიანობის მშვენიერი დემონსტრირებაა. იმის გამორკვევა, როგორ უნდა გადავჭრათ პრობლემა, მოსწავლის მხრიდან მოითხოვს – ლოგიკურ აზროვნებას, შაბლონების აღმოჩენას და ისეთ მოქმედებებს, რომლებიც მის სააზროვნო უნარებს განვითარებაში ეხმარება.
დაწყება
დახაზეთ 3X3 კვადრატი კალენდარზე (აუცილებელია, რომ კალენდრული დღეები მხოლოდ ერთ თვეს მოიცავდეს).
დაუსვით მოსწავლეებს კითხვა: რა შაბლონის/კავშირის დანახვა შეუძლიათ კალენდრის მოცემულ 3×3 კვადრატში?
ამ კითხვაზე მსჯელობას დაუთმეთ 5 – 10 წუთი. იმ შემთხვევაში თუ მოსწავლეებს დააინტერესდათ საკითხი ან მარტივად ვერ აღმოაჩინეს კავშირი, მაშინ შესაძლებელია, რომ ცოტა მეტი დროც დაუთმოთ ამ შეკითხვაზე მსჯელობას.
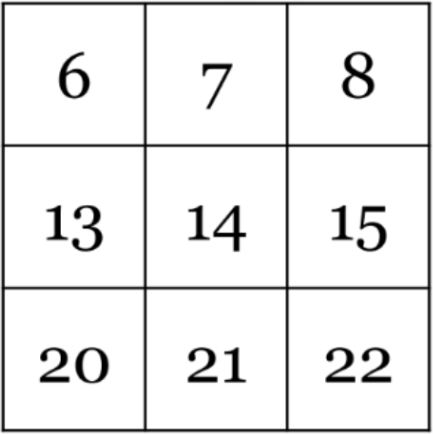
მას შემდეგ, რაც მოსწავლეები დაფიქრდებიან შესაძლო კავშირებზე, სთხოვეთ, რომ კვადრატში არსებული რიცხვები, რაც შეიძლება სწრაფად შეკრიბონ. ნებისმირ შემთხვევაში, თქვენ შეძლებთ, რომ მათზე სწრაფად შეკრიბოთ რიცხვები იმიტომ, რომ, დიდი ალბათობით, მათ გაუჭირდებათ კანონზომიერების მარტივად დანახვა, რომელიც თქვენთვის უკვე ნაცნობია. (ნახეთ მაგალითი კანონზომიერების გასაცნობად)
სამუშაო
მას შემდეგ, რაც მოსწავლეებს გააცნობთ კითხვას, მიეცით საშუალება იმუშავონ წყვილებში, რათა აღმოაჩინონ შაბლონები. თქვენ შეგიძლიათ, რომ სხვადასხვა ჯგუფს დააკვირდეთ, გაეცნოთ მათ იდეებს, საჭიროებისამებრ, მისცეთ სწორი მიმართულება და შეახსენოთ მარტივი კავშირის არსებობის შესახებ.
მინიშნება 1:
სხვადასხვა მაგალითის ცდა და მათში შაბლონების ძებნა ძალიან დაგვეხმარება. განსაკუთრებით იმ შემთხვევაში, თუ ის ორგანიზებულად იქნება ნაჩვენები. მაგალითად, თუ მოცემულ კალენდარზე, ნოემბრის თვეში მოვნიშნავთ სხვადასხვა კვადრატებს ასეთ შედეგს მივიღებთ:

კვადრატის ერთი უჯრით მარჯვნივ გადაადგილება, როგორც ჩანს, 9-ით ზრდის მთლიანი რიცხვების ჯამს. როგორ ფიქრობთ, ყოველთვის იმუშავებს ეს კანონზომიერება? რა მოხდება, თუ იგივე მოქმედებას გავაკეთებთ, ოღონდ სხვა თვეზე?
მინიშნება 2:
შეიძლება არსებობდეს რაიმე კანონზომიერება, თუ 2X2 კვადრატს გამოვიყენებთ 3X3-ის ნაცვლად? ანდაც, რა მოხდება, თუ მსგავს მოქმედებებისთვის 1X3 მართკუთხედს გამოვიყენებთ ?
მინიშნება 3:
არსებობს რაიმე გზა, რომელიც რიცხვების შეკრებას გაგვიადვილებს მათი მარტივ ნაწილებად დაშლით? რამდენად მარტივი იქნება, თუ თქვენ 3X3 კვადრატის ჯერ მწკრივებს შეკრებთ, ხოლო შემდეგ ერთმანეთს მიუმატებთ? ანდაც, ჯერ სვეტებს შეკრებთ და შემდეგ დაუმატებთ მათ ერთმანეთს?
შეჯამება
მოიხმეთ მოსწავლეები თავიანთი გადაწყვეტილებების გასაზიარებლად. ამ კითხვაზე პასუხის გაცემის მრავალი გზა არსებობს და შესაძლებელია, რომ მოსწავლეებს რამდენიმე ვარიანტი ჰქონდეთ.

ერთი შესაძლო შაბლონი ასეთია: რიცხვების ჯამი ყოველთვის 9-ჯერ მეტია კვადრატის ცენტრში არსებულ რიცხვზე. ეს იმიტომ ხდება, რომ კვადრატში მოქცეული რიცხვების ყოველი საპირისპირო წყვილი ცენტრში მდებარე რიცხვის საშუალოა. მაგალითად, 10-ისა და 12-ის შეკრების ნაცვლად, შეგვიძლია შევკრიბოთ ორი 11-იანი. 3-ისა და 19-ის შეკრების ნაცვლად, ჩვენ შეგვიძლია შევკრიბოთ ორი 11-იანი. ცხრავე რიცხვის შეკრება იგივე გამოდის, რაც შუა რიცხვის ცრაჯერ შეკრება, რაც მარტივად შეგვიძლია გამრავლების ოპერაცით ამოვხსნათ. ასე იოლადაა შესაძლებელი კვარდატში არსებული რიცხვების ჯამის გამოთვლა.
სააზროვნო კითხვები
- არსებობს, თუ არა მსგავსი შაბლონები 4X4-ზე კვადრატში რიცხვების სწრაფად შეკრებისთვის?
- შეგვიძლია, თუ არა, რომ მსგავსი კანონზომიერება აღმოვაჩინოთ ოთხკუთხედებში და არა – კვადრატში?
- კალენდრები ცოტა პატარაა. რა მოხდება, თუ 100 რიცხვიან დიაგრამაზე მოვნიშნავთ კვადრატს? ამ შემთხვევაშიც არსებობს მათი შეკრების სწრაფი გზა?
- რა არის 100 რიცხვიანი დიაგრამის ყველა რიცხვის ჯამი?
რჩევები
- მოსწავლეებისთვის იმის ცოდნა, რომ სწრაფად შეკრების გზა არსებობს, მაგრამ აღმჩენა სჭირდება დიდი მოტივატორია, შესაბამისად – არ გაამჟღავნოთ შაბლონი!
- დამატებითი კითხვები იმდენად ბუნებრივია, რომ ნამდვილად ღირს მათზე დროის დახარჯვა. ამ სავარჯიშოზე შესაძლებელია, რომ გაკვეთილის ნახევარზე მეტი დაიხარჯოს, თუმცა ინტერესის შემთხვევაში ნამდვილად ღირს ამ საკითხისთვის დროის დათმობა. ეს სავარჯიშო ერთ-ერთი საუკეთესო ხელსაწყოა იმისთვის, რომ მოსწავლეებმა თავად დაიწყონ მათემატიკურ კანონზომიერებებზე ფიქრი და მათი აღმოჩენა.