საკითხები: თვლა; მიმატება; გამოკლება; გეომეტრია; მონაცემები; ფართობი
მასალები: კვადრატული ფიგურები; უჯრებიანი ფურცლები
რამდენი კვადრატი გვჭირდება იმისთვის, რომ დიდი კვადრატები ავაშენოთ?
რატომ არის კარგი აქტივობა
კვადრატული ბლოკები ერთგვარი გზაა კონკრეტული თვლიდან აბსტრაქტულ გეომეტრიულ კანონზომიერებებამდე, გამრავლებამდე და გაყოფამდე მისასვლელად. ეს აქტივობა მოსწავლეებს საშუალებას აძლევს,აღმოაჩინონ ახალი იდეები.
დაწყება
აქტივობის დასაწყებად კვადრატული ბლოკებისგან ააწყე რამდენიმე კვადრატი, დათვალე რამდენი ბლოკი გჭირდება თითოეულის ასაწყობად და ჩაიწერე შედეგები. შემდეგ ჰკითხე კლასს: არის თუ არა რამე კანონზომიერება ბლოკების რაოდენობაში?
მაგალითი
შენ: მე მაქვს ყველა კვადრატული ბლოკი. მინდა, რომ მათგან კვადრატები ავაწყო. რა თქმა უნდა, შემიძლია კვადრატი ავაწყო ისე, რომ მხოლოდ ერთი ბლოკი გამოვიყენო. თუმცა, თქვენი აზრით, რამდენი ბლოკი დამჭირდება, იმისთვის რომ ცოტა უფრო დიდი კვადრატი ავაწყო? დაფიქრდით ამაზე და შემდეგ თქვენი მოსაზრება გაუზიარეთ თქვენს გვერდზე მჯდომს. [მოსწავლეები ჩურჩულებენ]. აბა, რამდენი ბლოკი დამჭირდება?
მოსწავლე: 4 ბლოკი
შენ: [აკეთებ დემონსტრაციას] გასაგებია, ასე უნდა დავაწყო. მოდი ახლა გავართულოთ. რამდენი ბლოკი დამჭირდება, რომ კიდევ უფრო დიდი კვადრატი ავაწყო? იმსჯელეთ 1 წუთის განმავლობაში და შემდეგ შევაჯამოთ. [მოსწავლეები მსჯელობენ].
შენ: გაქვთ რამე ვერსია?
მოსწავლეები: [მზად იყავით სხვადასხვა პასუხებისთვის] – 8, 12, 16, 9.
შენ: მაგარია! როგორც ჩანს რამდენიმე განსხვავებული პასუხი გვაქვს. მოდი დავიწყოთ რვით, ვინ ფიქრობს 8-ს? შეგიძლია გვაჩვენო როგორ ავაგოთ კვადრატი 8 ბლოკისგან? [მოხალისე მოსწავლეს სავარაუდოდ გამოუვა 2*4-ზე მართკუთხედი]. ესე იგი რვა ბლოკისგან გამოგვდის მართკუთხედი, თუმცა არა კვადრატი. შეგიძლიათ ვინმეს თქვათ, რატომ არ არის ეს კვადრატი? რა თვისება აქვს კვადრატს, რაც ამ ფიგურას არ აქვს?
მოსწავლე: ყველა გვერდი ტოლი უნდა იყოს.
შენ: მართალია. ყველა გვერდი ტოლი უნდა იყოს, აქ კი ერთი მხარე 2 კვადრატის გვერდის სიგრძისაა, ხოლო მეორე 4-ის. ეს არ არის კვადრატი. თუმცა, ჩემი აზრით შეგვიძლია გადავაწყოთ… [გადავაწყობთ 3*3-ზე კვადრატად, სადაც კუთხის ბლოკი აკლია]. ეს კვადრატია?
მოსწავლე: არა, ერთი აკლია!
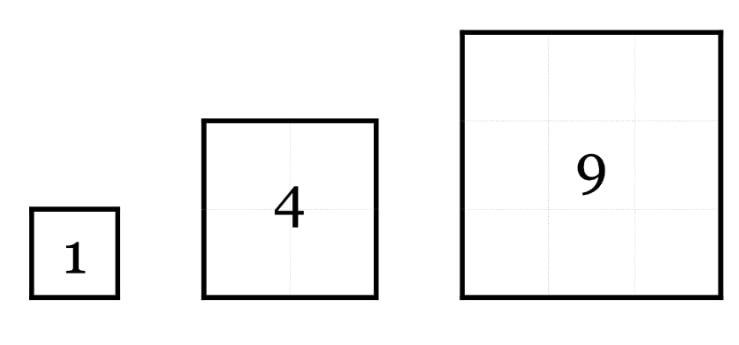
შენ: ესე იგი 8 ბლოკი არ გვეყოფა, 9 გვჭირდება! შეიძლება რაღაც კანონზომიერება იყოს. მოდი ჩავიწეროთ. [დაფაზე წერ: კვადრატები, რომლის აგებაც შეგვიძლია 1, 4, 9, …]
შენ: თქვენი დღევანდელი მისიაა, რომ ამ კანონზომიერებაში იპოვოთ მოცემული რიცხვები. რა რაოდენობის ბლოკები გვჭირდება, რომ კვადრატები ავაწყოთ? დარწმუნდით, რომ თქვენ ფიგურა ნამდვილად კვადრატი იქნება! ყველა გვერდი ტოლი უნდა იყოს. ასევე, ეცადეთ რომ არაფერი გამოტოვოთ, თუ შეგიძლიათ იპოვეთ ყოველი შემდეგი რიცხვი და არ გადაახტეთ უფრო მცირე კვადრატებს.
სამუშაო
მიეცი მოსწავლეებს 15-20 წუთი, რომ ააწყონ სხვადასხვა ზომის კვადრატები და ჩაიწერონ მათი ზომები. ასევე შეუძლიათ გამოიყენონ მათემატიკის რვეული და იქ ჩახატონ კვადრატები. როდესაც, მოსწავლეებს ექნებათ სია, შეადარებინეთ ისინი წყვილებში, რათა შეამოწმონ და მონიშნონ, აქვთ, თუ არა ერთნაირი რიცხვები. გამოიწვიე მოსწავლეები, ვისაც ჰგონია, რომ იპოვა კანონზომიერება, სთხოვე დახატვის გარეშე გამოიცნოს, რა იქნება შემდეგი რიცხვი. შემდეგ შეამოწმებინე ვარაუდი ნახატით ან ბლოკებით.
სააზროვნო კითხვები
- საიდან იცი, რომ ესაა შემდეგი, უფრო დიდი კვადრატი?
- საიდან იცი, რომ ამ რაოდენობით კვადრატი გამოვა?
- რა აქცევს კვადრატს კვადრატად?
- როგორ გააკეთე ეს კვადრატი? (წინა კვადრატი გამოიყენე საწყისად?)
- როგორ დაითვალე ბლოკები? (თითო-თითოდ, თუ სხვა გზით?)
- საიდან იცი, რომ თვლისას შეცდომა არ დაგიშვია?
- ყველა თანხმდება, რომ ეს სწორია?
შეჯამება
გააჩერე პროცესი და ჰკითხე მოსწავლეებს, რა რიცხვები მიიღეს. დასაწყისი უნდა გამოიყურებოდეს ასე: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …
იმსჯელეთ კანონზომიერებაზე, მიეცი მოსწავლეებს საშუალება, რომ სხვებს გააცნონ მათი ნაპოვნი კანონზომიერებები.
შეიძლება მიიღოთ შემდეგი შედეგები:
- ამ სიაში რიგრიგობითაა კენტი და ლუწი (კენტი, ლუწი, კენტი, ლუწი, ა.შ.)
- აკვირდებიან, რამდენით იზრდება ყოველი რიცხვი. კვადრატული რიცხვებისთვის ეს არის: +1, +3, +5, +7..
- აღმოაჩინონ, რომ მიღებული რიცხვებია: 1 × 1, 2 × 2, 3 × 3, 4 × 4, ა.შ.
დაუტოვე მოსწავლეებს შეკითხვა: როგორ შეიძლება, რომ ამ 3 კანონზომიერებიდან ყველა ერთდროულად სწორი იყოს?
რჩევები
- ღირს იმის ხსენება, რომ მიღებულ რიცხვებს, მათემატიკაში ვეძახით კვადრატულ რიცხვებს. ჰკითხეთ რამდენად კარგი სახელია ეს.
- კარგი იქნება, მოსწავლეებს აპოვნინო პირველი 10 კვადრატული რიცხვი, არაუშავს, თუ ყველა მოსწავლე ვერ ავა მაღალ რიცხვებზე. იმასაც არაუშავს, თუ ზოგი მოსწავლე არ ააწყობს ყველა კვადრატს და პირდაპირ დაწერს მაღალ რიცხვებს. რეალურად, მშვენიერია, თუ ამ ასაკში მსგავს კანონზომიერებას დაიჭერენ და დარწმუნებულები იქნებიან საკუთარ თავში. თუ რომელიმე რიცხვი გამოტოვეს, ისინი ამ კანონზომიერებით მარტივად შეძლებენ მის შევსებას.
- კიდევ ერთი საინტერესო კანონზომიერება კვადრატულ რიცხვებში არის ბოლო ციფრები, სადაც ვიღებთ განმეორებით სიმეტრიულ კანონზომიერებას (1, 4, 9, 6, 5, 6, 9, 4, 1, 0, 1, 4, 9, 6, ა.შ.). ზოგმა მოსწავლემ შეიძლება შეამჩნიოს ეს, თუმცა ამ კონტექსტში და ამ ასაკობრივ ჯგუფთან, უმჯობესია ამას არ ჩავუღმავდეთ და კითხვა პასუხგაუცემელი დავტოვოთ. თანაც ამით მოსწავლეებს მივცემთ საშუალებას, რომ თავისით ისწვალონ.