საკითხები: ლოგიკა; დედუქცია; არგუმენტაცია; კომუნიკაცია
მასალები: პატერნის ბლოკები; სამუშაო ფურცელი და ფანქარი
სასურველია ეს აქტივობა კონტრმაგალითების აქტივობის შემდეგ დაიწყოთ – “დაამტკიცე, რომ მასწავლებელი იტყუება”
რატომ არის კარგი აქტივობა
ეს სავარჯიშო ეხმარება მოსწავლეს კრეატიული აზროვნების განვითარებაში, ავარჯიშებს თვლის და შეკრება-გამოკლების უნარებს, ავითარებს გეომეტრიულ აზროვნებას და ეტაპობრივად გადადის მარტივიდან კომპლექსურ დავალებებზე.
დაწყება
წინასწარ მოამზადეთ ბლოკები: სამკუთხედი, ტრაპეცია, ექვსკუთხედი, რომბი.
დარწმუნდით, რომ ყველა მოსწავლეს მიუწვდება ხელი ბლოკებზე და დაიწყეთ გასახურებელი სავარჯიშოებით.
შეადგინეთ სამკუთხედი
- 5 ბლოკის გამოყენებით
- 10 ბლოკის გამოყენებით
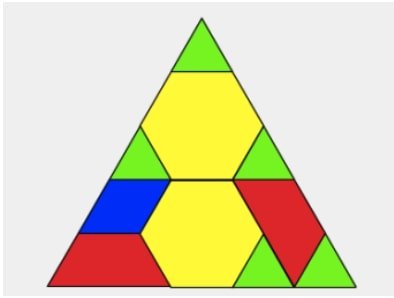
შეარჩიეთ ერთი მოსწავლის ნამუშევარი და აჩვენეთ მაგალითი, თუ როგორ უნდა გადაამოწმონ გამოყენებული ბლოკების რაოდენობა. მაგალითისთვის თუ ბლოკებით აწყობილი ფიგურა ქვემოთ მოყვენილი სამკუთხედია, მაშინ გამოსახულება ჩაიწერება შემდეგნაირად:
2 ექვსკუთხედი + 2 ტრაპეცია + 1 რომბი + 5 სამკუთხედი = 10 ბლოკი
როგორც კი მოსწავლეები ალღოს აუღებენ აქტივობას, დასვით სამიზნე შეკითხვა:
- შესაძლებელია თუ არა ნებისმიერი რაოდენობის ბლოკისგან სამკუთხედის აგება?
- დაასახელეთ ნებისმიერი რიცხვი რომელიც მოგინდებათ, მაგ. 3, 7, 812…
ჩამოწერეთ რიცხვები 1-დან 20-მდე, მოსწავლეებსაც იგივე გააკეთებინეთ, ისე რომ რიცხვებს შორის საკმარისი სივრცე იყოს. სასურველია ციფრები ვერტიკალურად ჩამოწეროთ, რათა, საჭიროების შემთხვევაში, გამოსახულების ჩატევა შევძლოთ.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
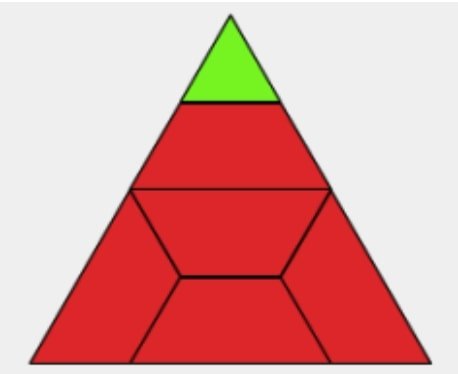
თუ მოსწავლეებს შეუძლია გააკეთონ სამკუთხედი ზემოთ მოყვანილი რომელიმე რაოდენობის ბლოკის მეშვეობით. მაგალითად: თუ მათ 6 ბლოკისგან შეუძლიათ გააკეთონ სამკუთხედი, ისე როგორც ნახატზეა, მაშინ ჩაწერონ გამოსახულებაც:
6 ბლოკი = 5 ტრაპეციას + 1 სამკუთხედი
გამოწვევა: ყველა რაოდენობის ბლოკისგან შეძლონ სამკუთხედის აწყობა და დააკვირდნენ არის თუ არა ისეთი რაოდენობა, რომლითაც შეუძლებელია სამკუთხედის აწყობა.
მოსწავლეებს შეუძლიათ იმუშავონ მარტო, ან მეწყვილესთან ერთად და ააწყონ სხვადასხვანაირი სამკუთხედები.
სააზროვნო კითხვები
- რამდენი ბლოკი გამოიყენე კონკრეტული სამკუთხედის ასაგებად?
- ჩაიწერე, თუ არა ამ ბლოკების რაოდენობა? მაჩვენე გამოსახულება.
- შეძელი, თუ არა აგეწყო სამკუთხედი თერთმეტი ბლოკისგან?
შეჯამება
აქტივობის მიღმა იმალება მნიშვნელოვანი გასააზრებელი მოდელი. მაგალითისთვის, ვთხოვოთ ბავშვებს რომ ტრაპეციები, რომელთაც აქვთ დიდი ფუძე (თან ავუხსნათ რას ნიშნავს) შეაერთონ ერთმანეთთან, მივიღებთ ექვსკუთხედს. შემდეგ ვთხოვოთ ერთ-ერთი სამკუთხედის ბლოკს გვერდებთან შეუერთონ ორი სამკუთხედის ბლოკი, რის შედეგადაც მიიღებენ ტრაპეციას. ორი ტრაპეციის შეერთებით კი შეეძლებათ ექვსკუთხედის მიღება. ეს დაეხმარებათ იმის დანახვაში რომ ნებისმიერი მონაკვეთებით აგებული შეკრული ტეხილის დაშლა შესაძლებელია სამკუთხედებად.
- უკვე არსებულ სამკუთხედზე რამდენი ბლოკის დამატება იქნება საჭირო რომ ახალი სამკუთხედი გამოვიდეს?
- უკვე არსებულ სამკუთხედის აწყობა შესაძლებელი არის თუ არა უფრო ნაკლები ბლოკით?
რჩევები
- ერთიდან ოცამდე რიცხვების ჩამოწერა და მათი შესაბამისი რაოდენობის ბლოკებით სამკუთხედების აწყობა წინ გადადგმული წარმატებული ნაბიჯია. ჯერ ვერ შესრულებული კი – გამოწვევა. ასე რომ, რთული ვარიანტები საფიქრალად დაუტოვეთ.
- ვინც წარმატებით ააწყობს სამკუთხედს 1-დან 20-მდე ყველა ბლოკის გამოყენებით, შესთავაზეთ ბლოკების გაზრდილი რაოდენობით, უფრო დიდი სამკუთხედის აწყობა.
- გამოიწვიეთ მოსწავლეები, სცადონ უკვე აწყობილი სამკუთხედის ზომაში გაზრდა, ისე რომ სამკუთხედი არ დაშალონ, აჩვენეთ ამის გაკეთების მართებული გზა.
- შესაძლებელია მომდევნო აქტივობისთვის დაავალოთ, შუაში (ასაწყობი სამკუთხედის შუაში) რაიმე ტიპის სიცარიელის დატოვებაც.
- თუ პირველ კლასელებთან აკეთებთ ამ აქტივობას, შეგიძლიათ სცადოთ მცირე რაოდენობის (მაგ. 1-10-მდე) ბლოკებით აწყობა.